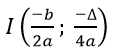Hàm số bậc hai là gì? Cách vẽ đồ thị hàm số bậc hai lớp 9, lớp 10

Bạn đang xem:
Hàm số bậc hai là gì? Cách vẽ đồ thị hàm số bậc hai lớp 9, lớp 10
tại nyse.edu.vn

Hàm bậc hai là gì? Cách làm bài tập hàm số lớp 9 lớp 10

Hàm bậc hai là gì? Cách vẽ đồ thị hàm số bậc hai các em đã được học trong chương trình Toán 9. Và lên lớp 10 tiếp tục học với kiến thức sâu hơn. Trong bài giảng hôm nay, trường THPT Chuyên Lê Hồng Phong sẽ trình bày ngắn gọn và giải thích các trường thông tin cần nhớ trong hàm số bậc hai này. Hãy chia sẻ!

I. TÁC PHẨM CAO CẤP LÀ GÌ?

Hàm bậc hai là một hàm có dạng y= ax2+bx+c trong đó a,b,c là các hằng số và #0. Hệ số hoàn toàn bình thường trong y. x và y lần lượt là các biến.

Bạn xem: Hàm số bậc hai là gì? Cách làm bài tập hàm số lớp 9 lớp 10

Tức là hàm số bậc hai chỉ cần thỏa mãn 2 điều kiện là có cực đại bậc 2 và ít nhất 1 hệ số khác 0.

Nếu có hai biến x và y thì hàm có dạng

f(x,y) = ax2+by2+cxy+dx+ey+f

sau đó, cùng với ví dụ công việc bình thường, chúng tạo ra trên một hệ thống hình nón khi được kết nối (parabolas, elip, đường tròn hoặc hyperbolas)

II. CÁCH RÚT NGUYÊN CÔNG TRÌNH BỔ SUNG

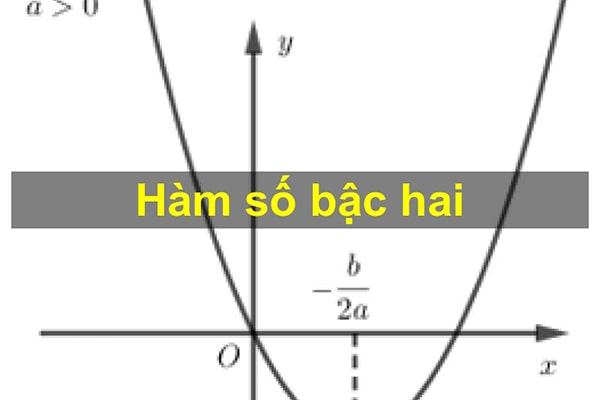
1. Cách vẽ đồ thị 9 hàm số bậc hai dạng y = ax2

Chúng tôi làm điều này theo trình tự:

Bước 1: Xác định tọa độ của đỉnh (0,0)
Bước 2: Xác định ít nhất năm điểm trên đồ thị để vẽ đồ thị chính xác nhất có thể.
3: Vẽ một parabol

Khi vẽ parabol cần chú ý đến dấu của hệ số a (a > 0 độ lõm quay, < 0 độ lõm giảm).

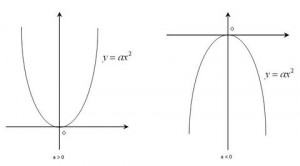
2. Cách vẽ đồ thị hàm số bậc hai lớp 10 dạng y = ax2+bx+c

Một. Học:

Bảng biến đổi của hàm số y=ax²+bx+c được chia thành 2 trường hợp:

Nếu a > 0 thì hàm số đồng biến theo thời gian (-∞; −b/2a) và đồng biến trên khoảng (-b/2a;+∞).

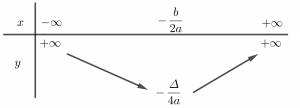
Với < 0, hàm số đồng biến trên khoảng (-∞; −b/2a) và nghịch biến trên khoảng (−b/2a;+∞).

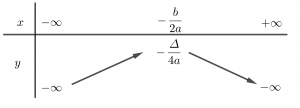
Đồ thị của hàm số bậc hai là một parabol.

b. Vẽ đồ thị hàm bậc hai

Để vẽ parabol y = ax2 + bx + c ta làm như sau:

Bước 1: Xác định tọa độ đỉnh
Phần 2: Xác định trục đối xứng x = (-b)/(2a) và khoảng cách từ mặt lõm của parabol.
Bước 3: Xác định chính xác các điểm của parabol (ví dụ: giao điểm của parabol với các trục song song và các điểm đối xứng tương ứng).
Bước 4: Dựa vào tính chất đối xứng, tính lồi lõm của parabol để vẽ parabol.

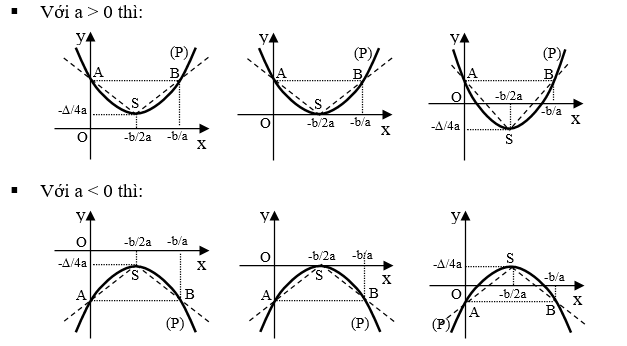
III. HOẠT ĐỘNG GIÁO DỤC CỦA TRƯỜNG THCS

BÀI 1:

Cho hàm số :y = f(x) = ax2 + 2x – 7 (P).

Tìm để đồ thị (P) đi qua A(1, -2)

PHẦN THƯỞNG.

Ta có: A(1, -2) (P), do đó -2 = a.12 + 2.1 – 7 a = 3

Vậy: y = f(x) = 3×2 + 2x – 7 (P)

BÀI 2:

Cho hàm số :y = f(x) = ax2 + bx + c (P).

Tìm a, b, c để đồ thị (P) đi qua A(-1, 4) và có đỉnh là S(-2, -1).

PHẦN THƯỞNG.

Ta có: A(-1, 4) (P) nên: 4 = a – b + c (1)

Ta có: S(-2, -1) (P) nên : -1 = 4a – 2b + c (2)

(P) có đỉnh S(-2, -1) nên : xS = $frac{-b}{2a}$ ⇔ 4a – b = 0 (3)

Từ (1), (2) và (3) ta có công thức:

⇔ $start{cases} a=5\b=20\c=19end{cases}$

Vậy: y = f(x) = 5×2 + 20x + 19 (P)

BÀI 3

Nhập bảng thay đổi và định cấu hình chức năng:

a) y = 3×2 – 4x + 1

d) y = -x2 – 4x – 4

Phần thưởng.

a)y = 3×2 – 4x + 1 (a = 3; b = -4; c = 1)

TXĐ:D=R.

Toạ độ đỉnh I(2/3; -1/3).

Trục đối xứng: x = 2/3

Cập nhật:

a = 3 > 0 hàm vi phân trên (-∞; 2/3). và đồng biến khoảng 2/3; +∞)

Bảng chuyển đổi:

x	-∞		2/3		+∞
y	+∞		-1/3		+∞

Những địa điểm đặc biệt:

(P) qua y = 0: 3×2 – 4x + 1 = 0 <=> x = 1 và x =

(P) nhảy dọc: x = 0 => y = 1

Hình ảnh:

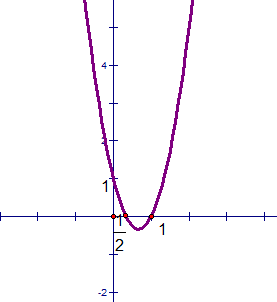
Đồ thị của hàm số y = 3×2 – 4x + 1 và parabol (P) là:

điểm I(2/3; -1/3).
Trục đối xứng: x = 2/3.
một parabol (P) bao quanh hang động trên bầu trời.

d) y = -x2 + 4x – 4

TXĐ:D=R.

Toạ độ Đỉnh I(2;0).

Trục đối xứng: x = 2

Cập nhật:

a = -1 < 0 hàm số đồng biến trên (-∞; 2). và ngắt khoảng 2; +∞)

Bảng chuyển đổi:

x	-∞		2		+∞
y	-∞		0		-∞

Những địa điểm đặc biệt:

(P) giao điểm của y = 0 : -x2 + 4x – 4 = 0 <=> x = 2

(P) qua đường thẳng: x = 0 => y = -4

Hình ảnh:

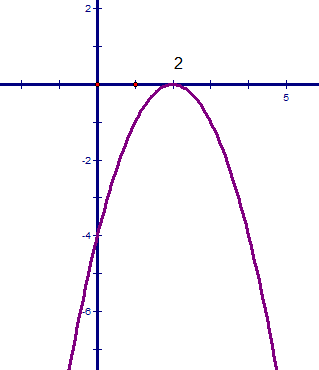
Đồ thị của hàm số y = -x2 + 4x – 4 và parabol (P) là:

đỉnh I(2;0).
Trục đối xứng: x=2.

một parabol (P) bao quanh hang ở phía dưới.

Bài 4: Cho hàm số y = x2 – 6x + 8

a) Tạo bảng chuyển tiếp và thực hiện các thao tác trên

b) Dùng đồ thị để biện luận dưới dạng phân số của m số điểm cách đều đường thẳng y = m và đồ thị của hàm số trên.

c) Dùng đồ thị, viết các khoảng thời gian hàm số chỉ nhận các số dương

d) Sử dụng đồ thị, tìm cực đại và cực tiểu đã cho ở trên [-1; 5]

PHẦN THƯỞNG:

a) y = x2 – 6x + 8

Chúng ta có:

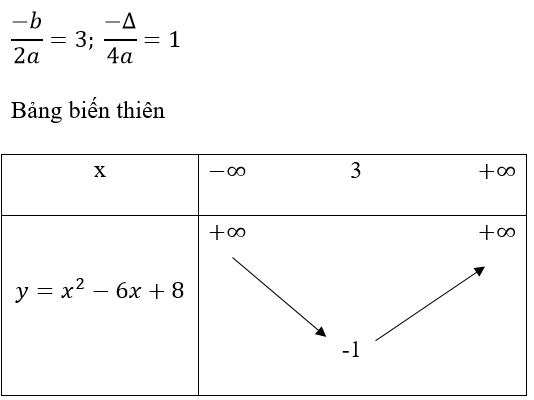
Cho đồ thị hàm số y = x2 – 6x + 8 có đỉnh I(3; -1) đi qua các điểm A(2; 0), B(4; 0).

Đồ thị của hàm số này nhận đường thẳng x = 3 làm điểm đối xứng và hướng thanh lên trên.

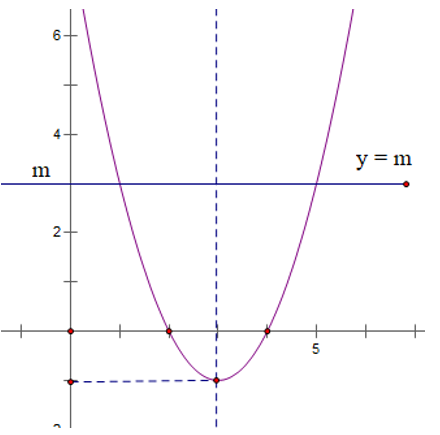
b) Đường thẳng y = m song song hoặc song song với trục hoành thì tuỳ thuộc vào đồ thị ta có.

Với m < -1, đường thẳng y = m và parabol y = x2 - 6x + 8 không cắt nhau.

Với m = -1 đường thẳng y = m và parabol y = x2 – 6x + 8 đi qua điểm (điểm chạm).

Với m > -1, đường thẳng y = m và parabol y = x2 – 6x + 8 đi qua hai điểm phân biệt.

c) Hàm số này nhận giá trị dương đối với phần đồ thị nằm trên trục hoành.

Do đó, hàm này chỉ nhận giá trị dương nếu x ∈ (-∞;2) ∪ (4; +∞).

d) Ta có y(-1) = 15; y(5) = 13; y(3) = -1, cộng với đồ thị của hàm dẫn xuất

BÀI 5: Nhận danh sách các hàm đảm bảo

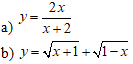
Phần thưởng:

a/ g(x) xác định khi x + 2 0 hoặc x -2

b/ h(x) xác định khi x + 1 ≥ 0 và 1 – x ≥ 0 hoặc -1 ≤ x ≤ 1. Vậy D = [-1;1]

BÀI TẬP 6: Xác định tỷ lệ chênh lệch của hàm số cho dưới đây:

Một)

Phần thưởng:

Một/

Đ = RẺ

ƒ(-x) = 3(-x)2-2 = 3×2 -2 = ƒ(x)

y là chức năng tương tự.

D = R{0}

y là một hàm lẻ.

c/ TXĐ :[0;+∞)isthesetofnenumsofnon-oddandoddnumbers[0;+∞)sisetiyofananirakoterontchitoyosikhalayodabwitsakapenayosamvetseka[0;+∞)whichisnotasymmetricsetofnon-evenandodd-numberednumbers[0;+∞)làtậphợpnênhàmsốkhônglạkhônglẻ[0;+∞)sisetiyofananirakoterontchitoyosikhalayodabwitsakapenayosamvetseka[0;+∞)khôngphảilàđốichiếuxứngnênhàmsốkhôngchẵnkhônglẻ[0;+∞)isthesetofnenumsofnon-oddandoddnumbers[0;+∞)sisetiyofananirakoterontchitoyosikhalayodabwitsakapenayosamvetseka[0;+∞)whichisnotasymmetricsetofnon-evenandodd-numberednumbers[0;+∞)làtậphợpnênhàmsốkhônglạkhônglẻ[0;+∞)sisetiyofananirakoterontchitoyosikhalayodabwitsakapenayosamvetseka[0;+∞) khôngphảilàtậpđốixứngnênhàmsốkhôngchẵnkhônglẻ

Bài 7:

Tìm độ lớn giao điểm của các đồ thị sau:

d: y = x – 1 và (P): y = x2 – 2x -1 .

Phần thưởng:

Xét phương trình giao điểm của (d) và (P):

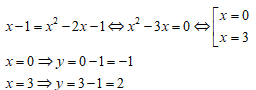
Vì vậy, hãy tạo giao điểm của (d) và (P) (0;-1) và (3,2).

Bài 8:

Lập bảng biến đổi hàm số, sau đó vẽ đồ thị của hàm số y = x2 – 4x + 3:

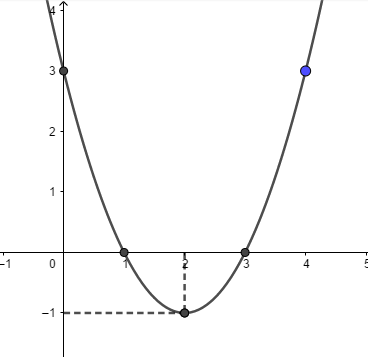
Phần thưởng:

a > 0 nên đồ thị hàm số này có cạnh lõm hướng lên

BBT

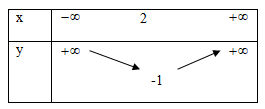
Hàm hiệp phương sai tại (2 ;∞) và hàm phương sai tại (-∞;2)

Đỉnh I(2;-1)

Trục đối xứng x = 2

Giao điểm của Oy và A(0,1)

Giao điểm với Ox là B(1;0); C(1/3;0)

Vẽ một parabol

Trên đây trường Học viện Anh ngữ toàn diện NYSE đã chia sẻ tới quý thầy cô và bạn đọc chủ đề Hàm số bậc hai là gì? Cách vẽ đồ thị hàm số lớp 9 lớp 10 chi tiết. Hy vọng bài viết đã cung cấp cho bạn những thông tin hữu ích để học tập. Tham khảo thêm nhiều màu tại link này!

Tác giả: Học viện Anh ngữ toàn diện NYSE

Thể loại: Giáo dục

Bài chia sẻ: https://c3lehongphonghp.edu.vn https://c3lehongphonghp.edu.vn/ham-so-bac-hai-la-gi-cach-ve-do-thi-ham-so-bac-hai- lop-9-lop-10/

Bạn thấy bài viết
Hàm số bậc hai là gì? Cách vẽ đồ thị hàm số bậc hai lớp 9, lớp 10
có khắc phục đươc vấn đề bạn tìm hiểu ko?, nếu ko hãy comment góp ý thêm về
Hàm số bậc hai là gì? Cách vẽ đồ thị hàm số bậc hai lớp 9, lớp 10
bên dưới đểHọc viện Anh ngữ toàn diện NYSE có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: nyse.edu.vn của Học viện Anh ngữ toàn diện NYSE

Nhớ để nguồn bài viết này:
Hàm số bậc hai là gì? Cách vẽ đồ thị hàm số bậc hai lớp 9, lớp 10
của website nyse.edu.vn

Chuyên mục: Giáo dục

[expander_maker more=”Xem thêm chi tiết về
Hàm số bậc hai là gì? Cách vẽ đồ thị hàm số bậc hai lớp 9, lớp 10
” less=”Read less”]