Lý thuyết hình bình hành. Cách chứng minh tứ giác là hình bình hành cực hay

Bạn đang xem:
Lý thuyết hình bình hành. Cách chứng minh tứ giác là hình bình hành cực hay
tại nyse.edu.vn

Lý thuyết hình bình hành. Làm thế nào để chứng minh một tứ giác là một hình bình hành lớn?

Khái niệm hình bình hành và cách chứng minh tứ giác là hình bình hành đã được học sinh tìm hiểu trong chương trình Toán 8, bài Hình học. Nhằm giúp các em chuẩn bị đủ thông tin cần nhớ từ khái niệm, tính chất, ký hiệu đến so sánh, chứng minh và nhiều hoạt động thực tiễn, trường THPT Chuyên Lê Hồng Phong chia sẻ bài viết dưới đây. Theo chúng tôi!

I. TÔN GIÁO PARANDALISE

1. Ý nghĩa

Bạn đang xem: Lý thuyết về hình bình hành. Làm thế nào để chứng minh một tứ giác là một hình bình hành lớn?

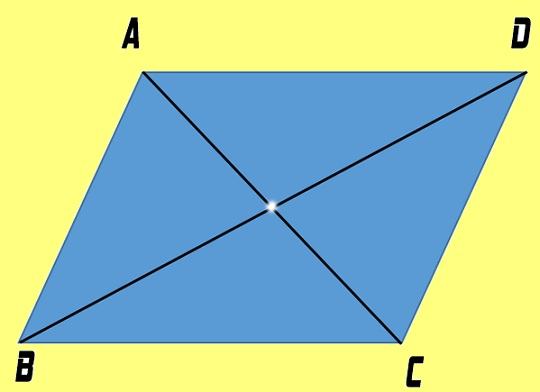
Hình bình hành là tứ giác có các cạnh đối diện.

ABCD là hình bình hành”>⇔ AB // CD và AD // BC.

Do đó, hình bình hành và hình thang có hai cạnh bằng nhau.

2. Tài sản

định lý:

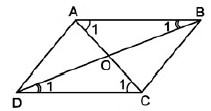
Trong một hình bình hành:

a) Các cạnh đối diện thì bằng nhau.

b) Các góc đối đỉnh thì bằng nhau.

c) Hai đường chéo đi qua trung điểm của mỗi đường.

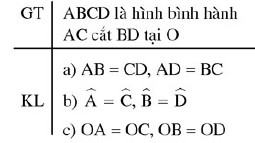
3. Dấu hiệu

Tứ giác có các cạnh bằng nhau là hình bình hành.
Tứ giác có các cạnh bằng nhau là hình bình hành.
Tứ giác có hai cạnh bằng nhau là hình bình hành.
Tứ giác có các góc bằng nhau là hình bình hành
Tứ giác có hai đường chéo đi qua mỗi cạnh là hình bình hành.

II. CÁCH CHO HÌNH ẢNH VÀ TÔN GIÁO

Để chứng minh một tứ giác là hình bình hành ta có thể sử dụng các phương pháp sau. Dựa vào dạng bài để áp dụng phương pháp chứng minh tứ giác là hình bình hành nội tiếp và chuẩn nhất nhé các em!

Bước 1: Chứng minh rằng các hình chữ nhật có các góc bằng nhau

Ví dụ: Cho tứ giác ABCD có ∆ABC = ∆ ADC và ∆BAD = ∆BCD. Chứng minh rằng ABCD là hình bình hành.

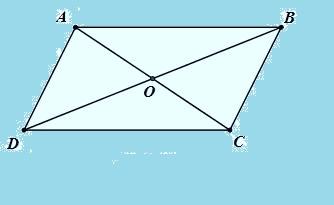
Dựa vào kết quả, ta có:

∆ABC = ∆ADC => Nợ ABC = Nợ ADC (1)

∆BAD = ∆BCD => Góc BAD = Góc BCD (2)

Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành vì các góc đối bằng nhau.

Cách 2: Chứng minh tứ giác có hai cạnh đối song song và bằng nhau

Ví dụ: Cho hình bình hành ABCD, gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BEDF là hình bình hành.

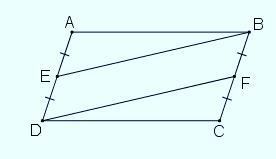
Chúng ta có:

ABCD là hình bình hành => AD // BC và AD = BC

AD // BC => DE // BF (1)

E là tâm của AD => DE = AD/2

F là trung điểm BC => BF = BC/2

Mà AD = BC (ABCD là hình bình hành)

DE = BF (2)

Từ (1) và (2) => Tứ giác DEBF là hình bình hành vì có hai cạnh đối diện bằng nhau và bằng nhau.

Bước 3: Chứng minh tứ giác có các cạnh bằng nhau

Ví dụ: Cho tứ giác ABCD có ∆ABC = ∆CDA. Chứng minh rằng ABCD là hình bình hành.

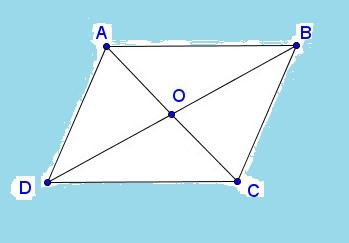
Dựa vào kết quả, ta có:

∆ABC = CDA => AD = BC và AB = CD

=> ABCD là hình bình hành có hai cạnh bên bằng nhau.

Bước 4: Chứng minh tứ giác có các cạnh bằng nhau

Ví dụ: Tứ giác ABCD có E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Tại sao?

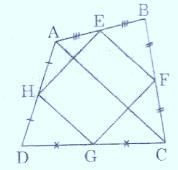
Chúng ta có:

EF là đường trung bình của tam giác ABC nên EF // AC (1)

Tương tự HG là đường trung tuyến của tam giác ACD nên HG // AC (2)

Từ (1) và (2) tìm HG // EF

Người khác:

FG là trung tuyến của tam giác CBD nên FG // BD (3)

Tương tự HE là đường trung tuyến của tam giác ABD nên HE // BD (4)

Từ (3) và (4) chứng minh HE // FG

Xét tứ giác EFGH và:

HG // EF và HE // FG;

Vậy tứ giác EFGH là hình bình hành vì các cạnh đối bằng nhau. (đcm)

Bước 5: Chứng minh tứ giác có hai đường chéo đi qua trung điểm của các cạnh.

Ví dụ: Cho hình bình hành ABCD. Gọi I, K lần lượt nằm giữa AB và CD. Các đường chéo BD lần lượt đi qua AK, AI tại M, N. Chứng minh rằng: AK // CI và DM = MN = NB

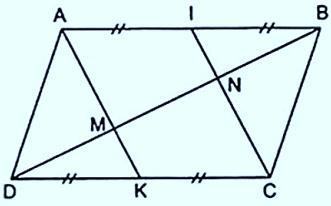
Chúng ta có:

AB // CD và AB = CD (do ABCD là hình bình hành)

I, K lần lượt là trung điểm của AB, DC => AI=IB và DK=KC.

Tứ giác AICK có hai cặp cạnh đối song song (AI và KC) nên AICK là hình bình hành nên AK // CI (cần xác định)

Ở đây chúng tôi có:

AM // MU và MK // NC

Hãy suy nghĩ ba lần AMB là:

AM // PA

AI = BI (I là trung điểm của AB)

IN là trung tuyến của tam giác AMB

N là trung điểm của MB => MN = NB (1)

Tương tự, hãy xem xét DNC ba lần:

MK// NC

DK = CK (K là tâm DC)

MK là trọng tâm tam giác DNC

M là trung điểm DN => DM = NM (2)

Từ (1) và (2) tìm được DM = MN = NB (điều cần chứng minh).

II. THỰC HÀNH LIÊN QUAN ĐẾN PARANDALISE

Bài tập 1: Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F. Chứng minh DEBF là hình bình hành.

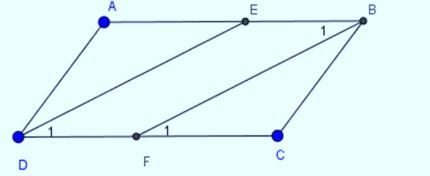
Chúng ta có:

Góc B1 = D1 là một trong hai góc bằng nhau B, D của đoạn thẳng ABCD

AB // CD (ABCD là hình bình hành) => Cạnh B1 = F1 (nội tiếp)

Nhưng 2 góc này bằng nhau => DE // BF

Xét tứ giác DEBF và:

DE // BF (chứng minh trên)

BE // DF (bởi AB // CD)

Do đó tứ giác DEBF là hình bình hành vì các cạnh tương ứng bằng nhau. (đcm)

Bài 2: Cho hình bình hành ABCD, các đường chéo AC và BD lần lượt đi qua O. Từ A kẻ AE vuông góc với BD, từ C kẻ CF vuông góc với BD. Chứng minh tứ giác AECF là hình bình hành.

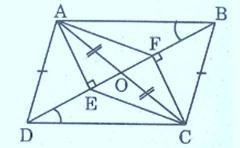
Chúng ta có:

OA = OC (tính chất hình bình hành) (1)

Xét tam giác vuông AEO và CFO có:

Góc AEO = Góc CFO = 90°

OA = OC

Góc AOE = Góc COF (đối diện)

Do đó, AEO = CFO (giả định – hằng số) => OE = YA (2)

Từ (1) và (2) suy ra tứ giác AECF là hình bình hành có hai đường chéo đi qua trung điểm của mỗi cạnh.

Bài tập 3: Cho hình 72. ABCD là hình bình hành

a) Chứng minh AHCK là hình bình hành

b) Gọi O là tâm HK. Chứng minh ba điểm A, O, C thẳng hàng.

Hồi đáp:

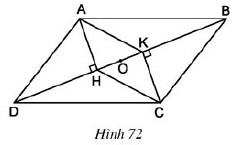
a) Các tam giác vuông AHD và CKD là:

AD = CB (gt)

∠D1 = B1 (phần bên trong)

Vậy AHD = CKB (góc nhọn, hai cạnh phụ)

Từ AH = CK

Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành,

b) Xét hình bình hành AHCK, tâm O nằm trên đường chéo của hình bình hành). Vậy ba điểm A, O, C thẳng hàng.

Bài tập 4: Cho tứ giác ABCD có E, F, G, H lần lượt nằm giữa các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Tại sao?

Hồi đáp:

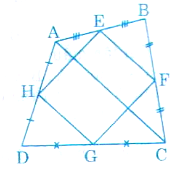
Tứ giác EFGH là hình bình hành.

Cách 1: EB = EA, FB = FC (gt)

nên EF là đường trung bình của ∆ABC.

Do đó EF // AC

Tương tự HG là tổng của ∆ACD.

Do đó HG // AC

EF // HG (1)

Tương tự với EH // FG (2)

Từ (1) và (2) suy ra EFGH là hình bình hành (đồng dạng 1).

Cách 2: EF là đường trung bình của ∆ABC nên EF = 1/2 AC.

HG là đường trung bình của ∆ACD nên HG = 1/2 AC.

Vậy EF = HG

EF // HG lại (đã xác nhận ở trên)

Do đó EFGH là hình bình hành (dấu 3).

Bài tập 5: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF

Hồi đáp:

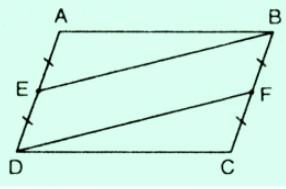
Chúng ta có:

DE = 1/2.AD; BF = 1/2.BC

Trong đó AD = BF (ABCD là hình bình hành)

=> DE = BF

Tứ giác BEDF bao gồm:

DE // BF (do AD // BC)

DE = BF

Vậy BEDF là hình bình hành lấy BE = DF

Bài tập 6: Cho hình bình hành ABCD. Gọi I, K lần lượt nằm giữa CD và AB. Đường chéo BD lần lượt đi qua AI, CK tại M, N. Đảm bảo rằng:

a) AI // CK

b) ĐM = MN = NB

Hồi đáp:

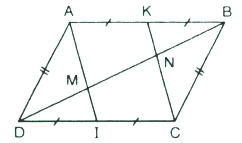
a) Tứ giác ABCD có AB = CD, AD = BC nên là hình bình hành.

Tứ giác AICK có AK // IC, AK = IC nên là hình bình hành.

Do đó AI // CK

b) ∆DCN có DI = IC, IM // CN.

(do AI // CK) phải giả sử DM = MN

Chứng minh tương tự cho ∆ABM ta có MN = NB.

Do đó DM = MN = NB

Bài 7: Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F.

a) Chứng minh rằng DE // BF

b) Tứ giác DEBF là hình gì? Tại sao?

Hồi đáp:

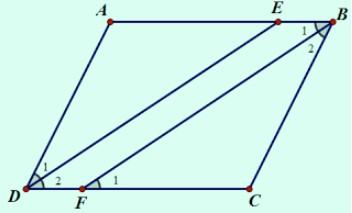
a) Ta có:

B^=D^”>Bˆ=Dˆ (Vì ABCD”>ABCDABCD là hình bầu dục) (1)

B1^=B2^=B2^”>B1ˆ=B2ˆ (vì BF”>BFBF là một phần của góc B”>BB) (2)

D1^=D2^=D^2″>D1ˆ=D2ˆ (vì DE”>DEDE là một phần của góc D”>DD) (3)

Từ (1), (2), (3) ⇒D2^=B1^”> ⇒D2 ˆ=B1ˆ được hai góc như sau: DE//BF”>DE//BFDE//BF

b) Tứ giác DEBF có:

DE // BF (chứng minh ở câu a)

BE // DF (vì AB // CD)

Vậy theo định nghĩa DEBF là hình bình hành.

Như vậy là các bạn vừa được tìm hiểu về lý thuyết hình bình hành, cách chứng minh một tứ giác là hình bình hành lớn và nhiều kiến thức bổ ích khác. Chúng tôi hy vọng thông tin này hữu ích cho bạn. Tham khảo cách chứng minh tứ giác là hình thoi tại link này!

Tác giả: Học viện Anh ngữ toàn diện NYSE

Chuyên mục: Giáo dục Chia sẻ: https://c3lehongphonghp.edu.vn https://c3lehongphonghp.edu.vn/ly-thuyet-hinh-binh-hanh-cach-chung-minh-tu-giac-la-hinh-bin- hanh – sữa /

Bạn thấy bài viết
Lý thuyết hình bình hành. Cách chứng minh tứ giác là hình bình hành cực hay
có khắc phục đươc vấn đề bạn tìm hiểu ko?, nếu ko hãy comment góp ý thêm về
Lý thuyết hình bình hành. Cách chứng minh tứ giác là hình bình hành cực hay
bên dưới đểHọc viện Anh ngữ toàn diện NYSE có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: nyse.edu.vn của Học viện Anh ngữ toàn diện NYSE

Nhớ để nguồn bài viết này:
Lý thuyết hình bình hành. Cách chứng minh tứ giác là hình bình hành cực hay
của website nyse.edu.vn

Chuyên mục: Giáo dục

[expander_maker more=”Xem thêm chi tiết về
Lý thuyết hình bình hành. Cách chứng minh tứ giác là hình bình hành cực hay
” less=”Read less”]