Bảng công thức Đạo hàm và Đạo hàm lượng giác [Đầy Đủ]

Bạn đang xem: Bảng công thức Đạo hàm và Đạo hàm lượng giác [Đầy Đủ]
tại nyse.edu.vn

Bảng Đạo hàm và Công thức Đạo hàm lượng giác [Đầy Đủ]

Đạo hàm và công thức lượng giác là một phần quan trọng trong kiến thức Toán 11, nhưng nó nhiều và phức tạp. Nếu không luyện tập thường xuyên, học sinh dễ quên. Trong bài viết hôm nay, trường THPT Chuyên Lê Hồng Phong sẽ điểm qua một cách cặn kẽ và toàn diện nhất những thông tin cần ghi nhớ. Vui lòng kiểm tra để lưu lại!

I. GIAI ĐOẠN NỮ

1. Từ được lấy từ cuốn sách là gì?

Bạn đang xem: Bảng Đạo Hàm Và Đạo Hàm Các Hàm Lượng Giác [Đầy Đủ]

Trong giải tích toán học, đạo hàm của một hàm thực chất là một phát biểu về sự thay đổi của hàm tại một điểm cho trước.

Trong vật lý, dòng điện biểu thị vận tốc tức thời của trường chuyển động hoặc dòng điện chạy qua dây dẫn.

Trong hình học, đạo hàm là hệ số góc của tiếp tuyến với đồ thị biểu diễn hàm số. Tiếp tuyến là biểu diễn gần nhất của hàm với giá trị của nó.

2. Thế nào là đạo hàm của một hàm số lượng giác?

Đạo hàm của một hàm lượng giác là một phương pháp toán học để tìm tỷ số giữa độ biến thiên của hàm lượng giác với độ biến thiên. Các hàm lượng giác phổ biến nhất là sin(x), cos(x) và tan(x).

II. TỐT NHẤT CỦA Đạo hàm lượng giác và Công thức đạo hàm

1. Định nghĩa đạo hàm, đạo hàm sơ cấp, đạo hàm cấp cao

2. Các lệnh ngoại vi cơ bản cần nhớ

3. Các file cơ bản cần nhớ

Từ f(x) trong đó x là một biến
Đạo hàm của f(u) trong đó u là một hàm số
Dẫn xuất từ các khu vực khác là rõ ràng

4. Bảng đạo hàm hàm số lượng giác và hàm số lượng giác ngược

+ Đạo hàm của các hàm lượng giác là một phương pháp toán học tìm tổng biến thiên của một hàm lượng giác theo sự thay đổi của lượng thay đổi. Các hàm lượng giác phổ biến nhất là sin(x), cos(x) và tan(x).

+ Biết đạo hàm của sin(x) và cos(x), ta dễ dàng tìm được đạo hàm của các hàm lượng giác còn lại vì chúng được biểu diễn bởi hai hàm trên, sử dụng quy tắc thương.

+ Phần chứng minh tích của sin(x) và cos(x) được giải thích bên dưới, từ đó có thể tính được tích của các hàm lượng giác khác.

+ Cách tính đạo hàm của các hàm lượng giác nghịch đảo và các hàm lượng giác thông dụng khác cũng được đưa ra dưới đây.

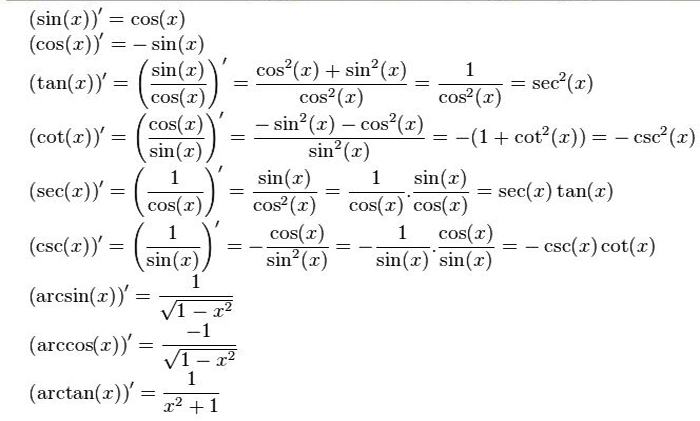
5. Danh sách đầu ra từ các đơn vị logic khác

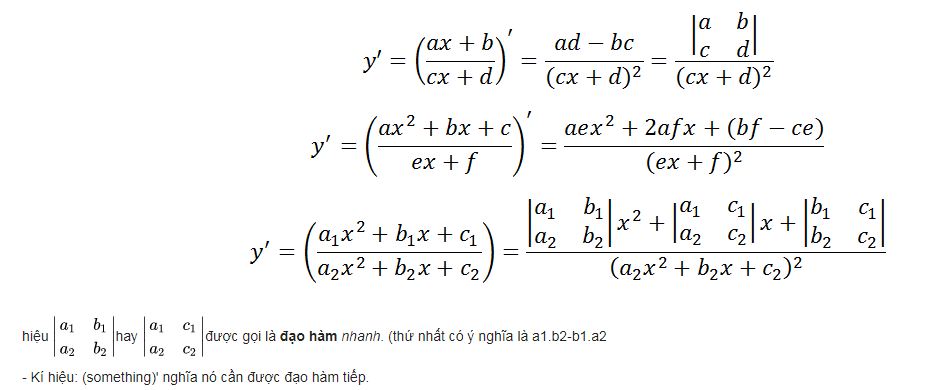
6. Bảng đạo hàm nâng cao

7. Bảng đạo hàm và viết tắt

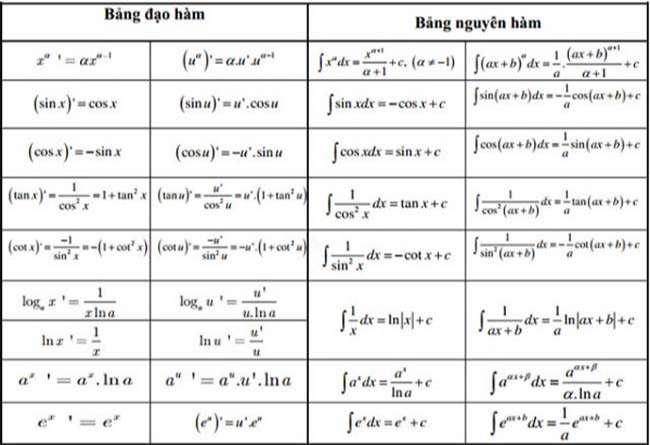
III. MÁY TÍNH ĐỌC

Máy tính bỏ túi là công cụ hữu ích để tính đạo hàm bậc nhất và bậc hai. Tính đạo hàm bằng máy tính bỏ túi cho kết quả chính xác hơn, thao tác đơn giản hơn như sau:

Tính toán các giá trị cơ sở:

Để tính toán đầu ra theo thứ tự thứ hai:

Nói công thức cho thứ n:

+ Bước 1: Tính đạo hàm cấp 1, đạo hàm cấp 2, đạo hàm cấp 3.

+ Bước 2: Tìm quy luật của hợp số, quy tắc dấu, hệ số, biến số, số mũ rồi rút ra cả phương trình

IV. TRẢI NGHIỆM HOẠT ĐỘNG SỐ

Bài 1:

Đạo hàm của hàm y = 1/ (cos²x – sin²x) là:

A. y’ = 2sin2x/cos²2x B. y’ = 2cos2x/cos²2x

C. y’ = cos2x/cos²2x D. y’ = sin2x/cos²2x .

Giải pháp:

y = 1/(cos²x – sin²x) = 1/cos2x.

Sử dụng quy tắc ngón tay cái để tính đạo hàm với (1/u)’ = -u’/u² ta được”

y’ = -(cos2x)’/ (cos2x)² = sin2x. (2x)’/cos²2x = 2sin2x.cos²2x.

Bài 2:

Cho hàm số y = cotx/2. Điều nào sau đây là đúng?

A. y² + 2y’ = 0 B. y² + 2y’ + 1 = 0

C. y² + 2y’ + 2 = 0 D. y² + 2y’ -1 = 0.

Giải pháp:

Ta có y’ = -1/(sin²x/2) = -1/2 (1+ cot²x/2).

Vậy y² + 2y’= cot²x/2 – 2.1/2(1 +cot²x/2) = cot²x/2 – (1 +cot²x/2) = -1 nên y² + 2y’ + 1 = 0. Chọn đáp án B.

Cách 2: Sử dụng máy tính casio.

Bước 1: Điều chỉnh vị trí của SHIFT MODE 4.

Thay x = 1 vào y = cotx/2 ta được y cot 1/2 ≈ 1

Dùng phím SHIFT ∫ nhập hàm y = cotx/2 và x = 1 để được kết quả ≈ -1.

Vậy y² + 2y’ + 1 = 0.

Bài 3:

Kết quả thứ n của hàm số y = cos2x là:

A. y(n) = (-1) ncos(2x + n π/2)

B. y(n) = 2 n cos(2x +π/2).

C. y(n) = 2n +1 cos(2x + nπ/2).

D. y(n) = 2n cos(2x + nπ/2).

Giải pháp:

Ta có y′=2cos(2x+π2),y′′=2²cos(2x+2π2)

y′′=2³cos(2x+3π2)

Bằng cách đó, chúng ta có thể xác định y(n)= 2ncos(2x+nπ2)

Bài 4:

Cho hàm số y= (x2+2x-1)/(2x-2). Tính đạo hàm của hàm này tại x= – 2

Giải pháp

Điều kiện: x≠1

Đối với bất kỳ hàm x≠1 nào có đầu ra là;

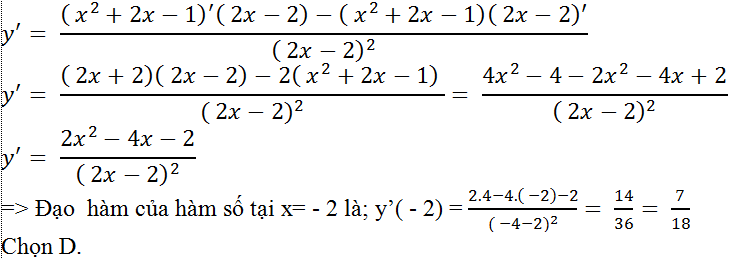
Tác giả: Học viện Anh ngữ toàn diện NYSE

Thể loại: Giáo dục

Bài chia sẻ: https://c3lehongphonghp.edu.vn https://c3lehongphonghp.edu.vn/bang-cong-thuc-dao-ham-va-dao-ham-luong-giac-day-du/

Bạn thấy bài viết Bảng công thức Đạo hàm và Đạo hàm lượng giác [Đầy Đủ]
có khắc phục đươc vấn đề bạn tìm hiểu ko?, nếu ko hãy comment góp ý thêm về Bảng công thức Đạo hàm và Đạo hàm lượng giác [Đầy Đủ]
bên dưới đểHọc viện Anh ngữ toàn diện NYSE có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: nyse.edu.vn của Học viện Anh ngữ toàn diện NYSE

Nhớ để nguồn bài viết này: Bảng công thức Đạo hàm và Đạo hàm lượng giác [Đầy Đủ]
của website nyse.edu.vn

Chuyên mục: Giáo dục

[expander_maker more=”Xem thêm chi tiết về Bảng công thức Đạo hàm và Đạo hàm lượng giác [Đầy Đủ]
” less=”Read less”]