Bất đẳng thức Bunhiacopxki: công thức, cách chứng minh và bài tập vận dụng

Bạn đang xem:
Bất đẳng thức Bunhiacopxki: công thức, cách chứng minh và bài tập vận dụng
tại nyse.edu.vn

Bất đẳng thức Bunhiacopsky: phương pháp, chứng minh và bài tập

Sự khác biệt của Bunhiacopsky là gì? Các dạng đó là gì, hệ quả của bất đẳng thức Bunhiacopxki, cách biểu diễn từng kết quả với các dạng bài hay và những phần kiến thức quan trọng, trường THPT Chuyên Lê Hồng Phong sẽ giải đáp qua bài viết dưới đây. . Bạn nhận được nó!

I. NHỮNG ĐIỂM LƯU Ý QUAN TRỌNG VỀ DẤU HIỆU BUNHIACOPXKI

1. Điểm khác biệt của Bunhiacopsky là gì?

Bạn có thể xem: Bất đẳng thức Bunhiacopsky: phương pháp, cách chứng minh và bài tập

Bất đẳng thức Bunhiacopxki còn được gọi là bất đẳng thức Cauchy – Bunhiacopxki – Schwarz, đây là một bất đẳng thức do ba nhà khoa học độc lập tìm ra và trình bày, nó có nhiều ứng dụng trong toán học. Ở nước ta, để phù hợp với tài liệu, trong tài liệu này chúng tôi cũng sẽ gọi nó là bất đẳng thức Bunhiacopski, được đặt theo tên của nhà toán học người Nga Bunhiacopski.

2. Phương pháp Bunhiacopsky

+ Bất đẳng thức cơ bản Bunhiacopsky:

$trái( {{a^2} + {b^2}} phải) trái( {{c^2} + {d^2}} phải) ge {trái( {ac + bd} phải)^2}$

Dấu “=” xảy ra khi và chỉ khi $frac{a}{c} = frac{b}{d}$

+ Bất đẳng thức Bunhiacopsky cho 2 bộ số:

Đó là hai bộ số $trái( {{a_1},{a_2},...,{a_n}} phải)$ Và $trái( {{b_1},{b_2},...,{b_n}} phải)$ Chúng ta có:

$trái( {a_1^2 + a_1^2 + ... + a_n^2} phải) trái( {b_1^2 + b_2^2 + ... + b_n^2} phải) ge {trái( {{a_1} } {b_1} + {a_2}{b_2} + ... + {a_n}{b_n}} phải)^2}$

Dấu “=” xảy ra khi và chỉ khi $frac{{{a_1}}}{{{b_1}}} = frac{{{a_2}}}{{{b_2}}} = ... = frac{{{a_n}}}{{{b_n}} }$

Nó là một phép hợp, nếu một số nào đó (i = 1, 2, 3, …, n) bằng không, thì nó bằng không.

3. Hệ quả của bất đẳng thức Bunhiacopsky

Kết quả 1:

Nếu như:

$[{a_1}{x_1} + ... + {a_n}{x_n} = C]$

Sau đó:

$[min(x_1^2 + ... + x_n^2) = frac{C}{{a_1^2 + ... + a_n^2}}]$

Hoàn thành khi:

$[frac{{{x_1}}}{{{a_1}}} = ... = frac{{{x_n}}}{{{a_n}}}]$

Kết quả 2: Nếu:

$[x_1^2 + ... + x_n^2 = {C^2}]$

Sau đó:

$[max({a_1}{x_1} + ... + {a_n}{x_n}) = left| C right|sqrt {a_1^2 + ... + a_n^2} ]$

thực hiện khi:

$[frac{{{x_1}}}{{{a_1}}} = ... = frac{{{x_n}}}{{{a_n}}} ge 0]$

$[min({a_1}{x_1} + ... + {a_n}{x_n}) = - left| C right|sqrt {a_1^2 + ... + a_n^2} ]$

Dấu “=” xuất hiện khi:

$[frac{{{x_1}}}{{{a_1}}} = ... = frac{{{x_n}}}{{{a_n}}} le 0]$

3. Tên loài Bunhiacopxki

Bất đẳng thức Bunhiacopski có các dạng sau:

Một. Hình thức cơ bản

b. định dạng nhỏ

Ở dạng trên, các tích của dạng 1, dạng 2, dạng 3 được gọi là bất đẳng thức Bunhiacopski và bất đẳng thức dạng 4 còn được gọi là bất đẳng thức Bunhiacopski.

c. Một số dạng đặc biệt

II. CÁCH KHÁC ĐỂ HIỂU BUNHIACOPXKI

1. Phương pháp chọn điểm rơi

Tương tự với bất đẳng thức Cauchy, khi sử dụng bất đẳng thức Bunhiacopsky để chứng minh bất đẳng thức ta phải giữ nguyên dấu của bất đẳng thức xảy ra, tức là phải biết mấu chốt của bài toán.

2. Phương pháp sử dụng bất đẳng thức Bunhiacopsky bậc nhất

Bất đẳng thức Bunhiacopskii ở dạng cơ bản là các bất phương trình biến thiên từ tổng (a1b1+a2b2+…+anbn)2 đến tổng (a21+a22+…+a2n)(b21+b22+…+b2n) hoặc ngược lại.

3. Phương pháp sử dụng bất đẳng thức Bunhiacopsky

Bất đẳng thức Bunhiacopsky là một bất đẳng thức có nhiều ứng dụng trong việc chứng minh các bất đẳng thức. Nó giải một tập hợp các bất phương trình có dạng phân số nào đó.

4. Phương pháp cộng trừ

Có những mâu thuẫn (hay các thuật ngữ để tìm WT, NN) nếu bỏ đi đôi khi rất khó hoặc không thể giải quyết được khi sử dụng mâu thuẫn Bunhiacopxki. Khi chúng ta gặp khó khăn trong việc thay đổi một số từ bằng cách thêm hoặc bớt số hoặc từ, chúng ta có thể dễ dàng sử dụng sự khác biệt của Bunhiacopski.

5. Quá trình biến đổi trong Bunhiacopxki

Có những mâu thuẫn nếu để như đã nêu thì rất khó tìm ra chứng cứ. Tuy nhiên, với một vài sửa đổi, chúng ta có thể đưa chúng về dạng quen thuộc bằng cách sử dụng bất đẳng thức Bunhiacopsky. Trong phần này, chúng ta sẽ nghiên cứu phương pháp quy đổi trong sai phân Bunhiacopsky.

Một cách kỹ thuật để thay đổi

III. YÊU CẦU KHÁC BIỆT BUNHIACOPXKI

Với ba bất phương trình a, b, c ta có thể sử dụng các phép biến đổi sau:

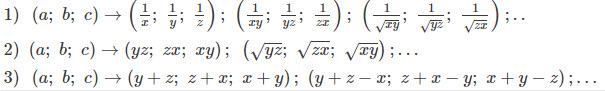
Đối với một số bất đẳng thức, người ta cho rằng chúng ta có thể thay đổi biến này:

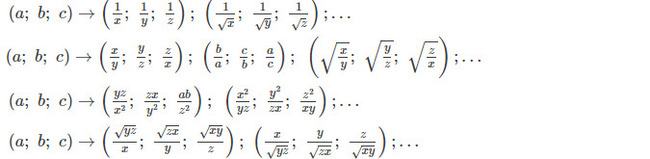
IV: BUNHIACOPXKI may thông thường

Gọi là số nguyên ≥ 2. Tìm giá trị nhỏ nhất của biểu thức:

A=a2+1a2A=a2+1a2

Khuyên nhủ:

V. CHẨN ĐOÁN MẸ TRÊN VẾT THƯƠNG CỦA BUNHIACOPXKI

Một. Bài tập và đáp án:

Bài tập 1: Cho a, b, c là các số thực. Đảm bảo rằng:

$sqrt {frac{{a + b}}{{a + b + c}}} + sqrt {frac{{b + c}}{{a + b + c}}} + sqrt {frac{{c + a ) ) }}{{a + b + c}}} le sqrt 6$

Hồi đáp:

Áp dụng bất đẳng thức Bunhiacopsky, ta có:

$1.sqrt {frac{{a + b}}{{a + b + c}}} + 1.sqrt {frac{{b + c}}{{a + b + c}}} + 1.sqrt { frac{{c + a}}{{a + b + c}}}$

$le sqrt {left( {{1^2} + {1^2} + {1^2}} phải) left( {frac{{a + b}}{{a + b + c}} + frac{{ b + c}}{{a + b + c}} + frac{{c + a}}{{a + b + c}}} ở bên phải)}$

$Leftrightarrow sqrt {frac{{a + b}}{{a + b + c}}} + sqrt {frac{{b + c}}{{a + b + c}}} + sqrt {frac{{c + a}}{{a + b + c}}} le sqrt {3.2} = sqrt 6$ (một cái gì đó để được xác nhận)

Dấu “=” xảy ra khi a = b = c

Bài 2: Tìm giá trị tuyệt đối của biểu thức $A = sqrt {x - 2} + sqrt {4 - x}$

Hồi đáp:

$A = sqrt {x - 2} + sqrt {4 - x}$

Trạng thái: $2 le x le 4$

Áp dụng bất đẳng thức Bunhiacopski, ta có:

${bên trái[ {1.sqrt {x - 2} + 1.sqrt {4 - x} } right]^2} trái ( {{1^2} + {1^2}} phải) trái ( {x - 2 + 4 - x} phải) = {2^2} = 4$

$start{array}{l} Rightarrow {A^2} le 4\ Leftrightarrow - 2 le A le 2 end{array}$

Tối đa = 2 lần $frac{1}{{sqrt {x - 2} }} = frac{1}{{sqrt {4 - x} }} Leftrightarrow x - 2 = 4 - x Leftrightarrow x = 3$ (thỏa mãn)

Vậy max A = 2 khi và chỉ khi x = 3

Bài tập 3: Chứng minh rằng nếu a, b, c là độ dài ba cạnh của một tam giác và p là nửa đường tròn thì $sqrt {p - a} + sqrt {p - b} + sqrt {p - c} le sqrt {3p}$

Hồi đáp:

Áp dụng bất đẳng thức Bunhiacopski, ta có:

$1.sqrt {p - a} + 1.sqrt {p - b} + 1.sqrt {p - c} le sqrt {trái( {{1^2} + {1^2} + {1^2}} phải) trái ( {p - a + p - b + p - c} phải)}$

$Leftrightarrow sqrt {p - a} + sqrt {p - b} + sqrt {p - c} le sqrt {3left( {3p - 2p} right)} = sqrt {3p}$ (một cái gì đó để được xác nhận)

Dấu “=” xảy ra khi và chỉ khi $frac{1}{{p - a}} = frac{1}{{p - b}} = frac{1}{{p - c}} Cột bên trái a = b = c$ hay tam giác đó có phải là tam giác đều không?

b. bài tập bổ sung

Bài 1: Tìm tổng của các từ sau:

Một, $A = sqrt {6 - x} + sqrt {x + 2}$

b $B = sqrt x + sqrt {2 - x}$

Bài tập 2: Cho a, b, c là các số thực cố định. Đảm bảo rằng:

$frac{a}{{sqrt {{a^2} + {b^2}}}} + frac{b}{{sqrt {{b^2} + {c^2}} }} + frac{c} {{sqrt {{c^2} + {a^2}}}} frac{3}{{sqrt 2}}$

(Gợi ý: đổi vế trái thành $sqrt {frac{{{a^2}}}{{{a^2} + {b^2}}}} + sqrt {{{b^2}}}{{{b^2} + { c^ 2}}}} + sqrt {{{c^2}}}{c^2} + {a^2}}}}$ rồi dùng bất đẳng thức Bunhiacopsky)

Bài tập 3: Cho a, b, c là các số thực, . Đảm bảo rằng:

$sqrt {a - 1} + sqrt {b - 1} + sqrt {c - 1} le sqrt {cleft( {ab + 1} right)}$

Bài 4: Cho a, b, c > 0 thỏa mãn abc = 1. Chứng minh:

$frac{1}{{a^3}left( {b + c} phải)}} + frac{1}{{b^3}left( {c + a} phải)}} + frac{1} { { {c^3}left({a + b}right)}} ge frac{3}{2}$

Bài 5: Cho x > 0 và y > 0 thỏa mãn x2 + y2 ≤ x + y. Xác nhận:

x +3 là +2 $sqrt{5}$

Như vậy các bạn vừa tìm hiểu định lý Bunhiacopsky: khái niệm, chứng minh và ứng dụng trong thực tế. Chúng tôi hy vọng, bằng cách chia sẻ bài viết này, bạn đã học được những thông tin quan trọng nhất về Đại số 9. Xem thêm sự khác biệt của Cosine tại liên kết này!

Tác giả: Học viện Anh ngữ toàn diện NYSE

Thể loại: Giáo dục

Bài chia sẻ: https://c3lehongphonghp.edu.vn https://c3lehongphonghp.edu.vn/bat-dang-thuc-bunhiacopxki-cong-thuc-cach-chung-minh-va-bai-tap-van-dung/

Bạn thấy bài viết
Bất đẳng thức Bunhiacopxki: công thức, cách chứng minh và bài tập vận dụng
có khắc phục đươc vấn đề bạn tìm hiểu ko?, nếu ko hãy comment góp ý thêm về
Bất đẳng thức Bunhiacopxki: công thức, cách chứng minh và bài tập vận dụng
bên dưới đểHọc viện Anh ngữ toàn diện NYSE có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: nyse.edu.vn của Học viện Anh ngữ toàn diện NYSE

Nhớ để nguồn bài viết này:
Bất đẳng thức Bunhiacopxki: công thức, cách chứng minh và bài tập vận dụng
của website nyse.edu.vn

Chuyên mục: Giáo dục

[expander_maker more=”Xem thêm chi tiết về
Bất đẳng thức Bunhiacopxki: công thức, cách chứng minh và bài tập vận dụng
” less=”Read less”]