Bất đẳng thức Cô-si: Lý thuyết cần ghi nhớ và các dạng bài tập thường gặp

Bạn đang xem: Bất đẳng thức Cô-si: Lý thuyết cần ghi nhớ và các dạng bài tập thường gặp
tại nyse.edu.vn

Kusagwirizana kwa Cosine: Lingaliro lokumbukira ndi mitundu yodziwika bwino ya masewera olimbitsa thupi

Kusalinganika kwa Cossian kapena AM-GM kusagwirizana ndi kufanana pakati pa chiwerengero cha masamu ndi kuchulukitsa kwa n nambala zenizeni zenizeni. Nkhani ya lero, Le Hong Phong High School ifotokoza zina zomwe muyenera kukumbukira za kusagwirizana kwa Cauchy ndi mitundu ina yamasewera olimbitsa thupi. Mwazindikira!

I. ZINTHU ZOYENERA KUKHALA M’MAKHANI A CHILENGEDWE CHA COSSIA

1. Kodi kusalingana kwa Cosine ndi chiyani?

Mukuyang’ana: Kusagwirizana kwa Cosic: Chiphunzitso Chokumbukira ndi Zochita Zolimbitsa Thupi

Dzina lolondola la kusalingana uku ndi kusalingana kwa AM-GM. Pali njira zambiri zotsimikizira chiphunzitsochi, koma chabwino kwambiri ndi umboni wa Cauchy.

Mu masamu, kusagwirizana kwa Cauchy ndi kufananiza kusiyana pakati pa chiwerengero cha masamu ndi kuchulukitsa kwa n nambala zenizeni zomwe sizili zoipa.

Kutanthauzira kwa masamu a n nambala zenizeni zenizeni nthawi zonse zimakhala zazikulu kuposa kapena zofanana ndi kuchulukitsa kwawo, ndipo tanthauzo la masamu ndilofanana ndi kuchulukitsa kokha ngati n’zofanana.

+ Njira:

– Kusagwirizana kwa Cosi ndi manambala 2 omwe si olakwika:

$frac{{a + b}}{2} ge sqrt {ab}$

Chizindikiro “=” chimapezeka ngati a = b

– Kusagwirizana kwa Cosi kwa manambala enieni omwe si olakwika:

$frac{{{x_1} + {x_2} + ... + {x_n}}}{n} ge sqrt[n]{{{x_1}{x_2}... {x_n}}}$

Chizindikiro cha “=” chimapezeka ngati ndipo ngati ${x_1} = {x_2} = ... = {x_n}$

2. Mitundu yotchulidwa ya kusalingana kwa Cosine

a. Mtundu wamba wa kusalingana kwa Cossian

Perekani $mawonekedwe {{x}_{1}},{{x}_{2}},{{x}_{3}}lddots {{x}_{n}}$ ndi manambala enieni, tili ndi:

– Fomu 1: $displaystyle frac{{{{x}_{1}}+{{x}_{2}}+ldots +{x}_{n}}}}{n}ge sqrt{{{x}_{ 1}}cdot {{x}_{2}}cdots {{x}_{n}}}}$

– Fomu 2: $mawonekedwe {{x}_{1}}+{{x}_{2}}+ldots +{x}_{n}}ge ncdot sqrt[n]{{{{x}_{1}}cdot {{x}_{2}}cdots }}$

– Fomu 3: $mawonekedwe {{kumanzere({frac{{{x}_{1}}+{{x}_{2}}+ldots +{{x}_{n}}}}{n}} kumanja)}^ {n}}ge {{x}_{1}}cdot {{x}_{2}}cdots {{x}_{n}}$

– Fomu 4: $displaystyle dfrac{1}{{x_{1}}+dfrac{1}{{x_{2}}+ldot +dfrac{1}{{x_{n}}}}^{text{3}}ge dfrac {{n^{2}} {{x_{1}+x_{2}+ldots x_{n}}}$

– Fomu 5: $mawonekedwe amanzere( {x_{1}+x_{2}+lddots x_{n}} kumanja) kumanzere( {dfrac{1}{{x_{1}}}+dfrac{1}{{x_{2}}} +ldots +dfrac{1}{{x_{n}}}} kumanja)ge n^{2}$

Chizindikiro chofanana chimachitika pokhapokha ngati $mawonekedwe {{x}_{1}}={{x}_{2}}=cdots ={{x}_{n}}$

b. Mtundu wapadera wa kusiyana kwa Cosine

Ndi zochitika zapadera zomwe zili pamwamba pomwe n=2, n=3.

c. Zosagwirizana zina zimachokera ku kusagwirizana kwa Cauchy

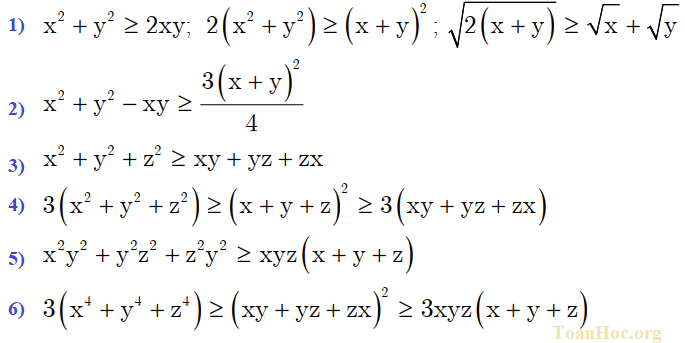
d. Samalani mukamagwiritsa ntchito AM – GM

Mukamagwiritsa ntchito kusalinganika kwa cosic, manambala sayenera kukhala opanda cholakwika
Kusagwirizana kwa Cosic kumagwiritsidwa ntchito nthawi zambiri mu BDT ndikofunikira kutsimikizira kuti pali kuchuluka ndi mankhwala
Mkhalidwe wa kupezeka kwa ‘=’ chizindikiro ndi manambala ofanana
Kusagwirizana kwa cosic kumakhalanso ndi mawonekedwe osazolowereka omwe amagwiritsidwa ntchito nthawi zambiri

Kwa manambala awiri:

x2+y2≥2xy.
x2+y2≥(x+y)22
xy≤(x+y2)2

Kwa manambala atatu: abc≤a3+b3+c33,abc≤(a+b+c3)3

3. Zotsatira za kusagwirizana kwa Cossi

+ $displaystyle {{x}^{2}+{{y}^{2}}ge 2xy;2left({{x}^{2}}+{{y}^{2}}} kumanja)ge { {kumanzere({x+y} kumanja)}^{2}};sqrt{{2left({x+y} kumanja)}}ge sqrt{x}+sqrt{y}$

+ $displaystyle {{x}^{2}+{{y}^{2}}-xyge frac{{3{{{left({x+y} kumanja)}}}^{2}}}}{4}$

+ $mawonekedwe {{x}^{2}+{{y}^{2}}+{{z}^{2}}ge xy+yz+zx$

+ $displaystyle 3 left( {{x}^{2}+{{y}^{2}}+{{z}^{2}}} kumanja)ge {{left( {x+y+z} kumanja) }^{2}}ge 3 kumanzere( {xy+yz+zx} kumanja)$

+ $mawonekedwe {{x}^{2}}{{y}^{2}+{{y}^{2}}{{z}^{2}}+{{z}^{2}}{{ y}^{2}}ge xyzleft( {x+y+z} kumanja)+3kumanzere( {{x}^{4}}+{{y}^{4}}+{{z}^{4 }}} kumanja)ge {{left( {xy+yz+zx} kumanja)}^{2}}ge 3xyzleft( {x+y+z} kumanja)$

4. Umboni wa Cauchy

a. Milandu yomwe zikhalidwe zonse ndizofanana

Ngati ma values onse ndi ofanana:

i.e. kuchuluka kwawo kuli nx1, ndiye tanthauzo xchoyamba; ndipo chopangidwa ndi manambala pansi pa sikweya mizu ndi xchoyambankotero kuti kuchulukitsidwa tsopano kuli xchoyamba; chotero, woyamba ndi wachiwiri ali ofanana, zomwe ziyenera kutsimikiziridwa.

b. Milandu yomwe zikhalidwe sizili zofanana

Ngati zikhalidwe zonse zofananira sizili zofanana, ndiye kuti tanthauzo lake ndi lalikulu kuposa tanthauzo lochulukitsa. Mwachiwonekere, izi zingatheke pokhapokha n> 1. Mlanduwu ndi wovuta kwambiri ndipo wagawidwa m’magawo ambiri kuti atsimikizire.

c. Nkhani n = 2

Ngati n= 2, kutanthauza kuti pali mfundo ziwiri x1 ndi x2, ndipo kuchokera pamalingaliro apamwambawa, tili ndi:

0 \[3pt] x_1^2 – 2 x_1 x_2 + x_2^2 & > 0 \[3pt] x_1^2 + 2 x_1 x_2 + x_2^2 & > 4 x_1 x_2 \[3pt] kumanzere( x_1 + x_2 kumanja) ^2& > 4 x_1 x_2 \[3pt] Bigl( frac{x_1 + x_2}{2} Chachikulu)^2 & > x_1 x_2 \[3pt] frac{x_1 + x_2}{2} & > sqrt{x_1 x_2} mapeto{align} “>

chinthu chotsimikizira.

d. Mlandu n = 2k

Ganizirani milandu n= 2 kndi k ndi chiwerengero chabwino. Timapitilira ndikulowetsa masamu.

M’malo mwake,k = 1 ndi n = 2, kusalingana kwatsimikiziridwa pamwambapa.

Pamene, pali phindu k> 1 iliyonse, poganiza kuti kusalingana kumagwira ntchito n = 2k−1, ndipo akuyenera kutsimikizira kuti ndizoonadi liti n = 2k. Kuti muchite izi, tsatirani izi:

$kuyamba{align} frac{x_1 + x_2 + cdots + x_{2^k}}{2^k} & {} =frac{frac{x_1 + x_2 + cdots + x_{2^{k-1}}}{ 2^{k-1}} + frac{x_{2^{k-1} + 1} + x_{2^{k-1} + 2} + ma cdots + x_{2^k}}{2^{ k-1}} {2} \[7pt] & ge frac{sqrt[2^{k-1}]{x_1 x_2 ma cdots x_{2^{k-1}}} + sqrt[2^{k-1}]{x_{2^{k-1} + 1} x_{2^{k-1} + 2} ma cdots x_{2^k}}}{2} \[7pt] & ge sqrt{sqrt[2^{k-1}]{x_1 x_2 ma cdots x_{2^{k-1}}} sqrt[2^{k-1}]{x_{2^{k-1} + 1} x_{2^{k-1} + 2} ma cdots x_{2^k}}} \[7pt] ndi = sq[2^k]{x_1 x_2 ma cdots x_{2^k}} mapeto{align}$

kwa kusalingana koyamba, mbali zonse ziwiri ndi zofanana pokhapokha ngati zonsezi zili zoona:

$x_1 = x_2 = ma cdots = x_{2^{k-1}}$
$x_{2^{k-1}+1} = x_{2^{k-1}+2} = madoti = x_{2^k}$

(Pankhaniyi, tanthauzo loyamba la masamu ndi kuchulukitsa koyamba ndix1, ndi chimodzimodzi kwa masamu achiwiri amatanthauza ndi 2nd kuchulukitsa zikutanthauza); ndipo mu kusalingana kwachiwiri, mbali ziwirizo ndi zofanana pokhapokha ngati zikhalidwe ziwirizo ndizofanana. Chifukwa si onse 2 k ndi ofanana, sikutheka kuti kusagwirizana kulikonse kukhale kofanana, kotero tikudziwa kuti:

sqrt[2^k]{x_1 x_2 ma cdots x_{2^k}}”>

(zomwe ziyenera kutsimikiziridwa).

e. Mlandu n <2k

Ngati n Sichidziwitso chachirengedwe ku maziko a 2, ndiye kuti ndi yaying’ono kwambiri kuposa chiwerengero china mwachibadwa ku maziko a 2, popeza mndandanda wa 2, 4, 8,,…, 2k.. sichinatsekeredwa. Choncho, popanda kutaya zonse, ndi m mtengo womwe umamvera kutanthauzira kwachilengedwe ku maziko a 2 kuposa n.

Kotero ngati ife tiri nazo n nambala, ndiye titha kufotokoza tanthauzo la α, ndikukulitsidwa motere:

$x_{n+1} = x_{n+2} = ma cdots = x_m = alpha.$

Kenako tili ndi:

sqrt[m]{x_1 x_2 ma cdots x_n x_{n+1} ma cdots x_m} \[6pt] ndi = sq[m]{x_1 x_2 cdots x_n alpha^{mn}}, mapeto{align} “>

choncho

x_1 x_2 cdots x_n alpha^{mn} \[5pt] alpha^n & > x_1 x_2 ma cdots x_n \[5pt] alpha & > sqrt[n]{x_1 x_2 ma cdots x_n} mapeto{align} “>

chinthu chotsimikizira.

II. ZOCHITA KAWIRIKAWIRI MITUNDU YA CHILENGEDWE CHA COSCIENCE

a. Zochita zolimbitsa thupi ndi mayankho:

Phunziro 1: Pezani mtengo wochepera wa mawuwo $A = x + frac{7}{x}$ ndi x>0

Yankho:

Ikani kusiyana kwa Cosi pa manambala awiri x> 0 ndipo tili ndi:

$x + frac{7}{x} ge 2sqrt {x.frac{7}{x}} = 2sqrt 7$

Chizindikiro “=” chimapezeka ngati ndipo pokhapokha ngati $x = frac{7}{x} Mzere wamanzere {x^2} = 7 Leftrightarrow x = sqrt 7$ (chifukwa x> 0)

Ndiye min $A = 2sqrt 7 Leftrightarrow x = sqrt 7$

Ntchito 2: Lolani x > 0, y > 0 kukhutiritsa chikhalidwecho $frac{1}{x} + frac{1}{y} = frac{1}{2}$ . Pezani kuchuluka kwa mawuwo $A = sqrt x + sqrt y$

Yankho:

Kugwiritsa ntchito kusalingana kwa Cosi ku manambala awiri x > 0, y > 0 tili ndi:

$frac{1}{x} + frac{1}{y} ge 2sqrt {frac{1}{x}.frac{1}{y}}$

$Leftrightarrow frac{1}{2} ge frac{2}{{sqrt {xy} }} Leftrightarrow sqrt {xy} ge 4$

Apanso, kugwiritsa ntchito kusalingana kwa Cosi kwa manambala awiri x > 0, y > 0 tili ndi:

$sqrt x + sqrt y ge 2sqrt {sqrt {xy} } = 2sqrt 4 = 4$

Chizindikiro “=” chimapezeka ngati ndipo pokhapokha ngati $left{start{array}{l} x = y\ frac{1}{x} + frac{1}{y} = frac{1}{2} end{array} kumanja. Leftrightarrow x = y = 4$

Kotero minA = 4 ngati ndipo kokha ngati x = y = 4

Phunziro 3: Tsimikizirani kuti ndi manambala atatu omwe si otsutsa a, b, c okhutiritsa a + b + c = 3, ndiye:

$frac{a}{{b + c}} + frac{b}{{c + a}} + frac{c}{{a + b}} ge frac{3}{2}$

Ndemanga: Vuto limakwaniritsa chizindikiro chofanana ngati ndi chi pamene a = b = c = 1. Tidzagwiritsa ntchito njira yolamulira ndi kuchepetsa motere:

Yankho:

Kugwiritsa ntchito kusalingana kwa Cosi ku manambala atatu omwe si otsutsa a, b, c kuli:

$frac{a}{{b + c}} + frac{{b + c}}{4} + frac{1}{{2a}} ge 3sqrt[3]{{frac{a}{{b + c}}.frac{{b + c}}{4}.frac{1}{{2a}}}} = 3sqrt[3]{{frac{1}{8}}} = frac{3}{2}$

Ifenso tatero $frac{b}{{c + a}} + frac{{c + a}}{4} + frac{1}{{2b}} ge frac{3}{2}$ ndi $frac{c}{{a + b}} + frac{{a + b}}{4} + frac{1}{{2c}} ge frac{3}{2}$

Powonjezera mbali zonse tili ndi:

$frac{a}{{b + c}} + frac{{b + c}}{4} + frac{1}{{2a}} + frac{b}{{c + a}} + frac{{c + a}}{4} + frac{1}{{2b}} + frac{c}{{a + b}} + frac{{a + b}}{4} + frac{1}{{2c} } ge 3.frac{3}{2} = frac{9}{2}$

$Leftrightarrow frac{a}{{b + c}} + frac{b}{{c + a}} + frac{c}{{a + b}} + frac{{2left( {a + b + c} kumanja )}}{4} + frac{{ab + bc + ca}}{{2abc}} ge frac{9}{2}$

$Leftrightarrow frac{a}{{b + c}} + frac{b}{{c + a}} + frac{c}{{a + b}} + frac{{a + b + c}}{2} + frac{{a + b + c}}{2} ge frac{9}{2}$

$Leftrightarrow frac{a}{{b + c}} + frac{b}{{c + a}} + frac{c}{{a + b}} ge frac{9}{2} - 3 = frac{3 {2}$

Chizindikiro “=” chimapezeka ngati a = b = c = 1

b. Zolimbitsa thupi zowonjezera:

Ntchito 1: Pezani mtengo wochepera wa mawu awa:

a, $B = frac{{kumanzere({x + 4} kumanja)kumanzere({x + 9} kumanja)}}{x}$ ndi x>0

(chidziwitso: kusintha $B = frac{{kumanzere({x + 4} kumanja)kumanzere({x + 9} kumanja)}}{x} = frac{{{x^2} + 13x + 36}}{x} = x + 13 + frac{{36}}{x}$ ndiye gwiritsani ntchito kusalingana kwa Cosi)

b, $C = frac{{{{kumanzere({x + 10} kumanja)}^2}}}{x}$ ndi x>0

c, $D = frac{x}{3} + frac{3}{{x - 2}}$ ndi x>2

(Chidziwitso: sinthani ndikuyika kusalingana kwa Cosi)

Phunziro 2: Pezani mtengo wochepera wa mawuwo $P = x + frac{1}{y} + frac{4}{{x - y}}$ ndi x>y>0

(chidziwitso: kusintha $P = x - y + frac{4}{{x - y}} + y + frac{1}{y}$ )

Ntchito 3: Ndi a, b, c kukhala manambala enieni osakhala negative, tsimikizirani:

$kumanzere( {a + b + c} kumanja) kumanzere( {frac{1}{a} + frac{1}{b} + frac{1}{c}} kumanja) ge 9$

(umboni woti mugwiritse ntchito kusiyana kwa Cosi pa manambala atatu a, b, c omwe siwolakwika)

Ntchito 4: Kupatsidwa manambala enieni atatu a, b, c okhutiritsa a + b + c = 3. Tsimikizirani kuti:

$frac{{b + c}}{a} + frac{{c + a}}{b} + frac{{a + b}}{c} ge 6$

(apangitse kugwiritsa ntchito njira yolamulira)

Chifukwa chake mwaphunzira kumene chiphunzitso ndi mitundu yodziwika bwino yamasewera a Cosine kusalingana. Tikukhulupirira, pogawana naye, mumvetsetsa bwino chidziwitso chofunikira kwambiri cha Algebra 9. Onani zosintha zambiri zamawu okhala ndi masikweya mizu pa ulalowu!

Wolemba: Le Hong Phong High School

Category: Maphunziro

Nkhani yogawana: https://c3lehongphonghp.edu.vn https://c3lehongphonghp.edu.vn/bat-dang-thuc-co-si-ly-thuyet-can-ghi-nho-va-cac-dang-bai – tap-thuong-gap/

Bạn thấy bài viết Bất đẳng thức Cô-si: Lý thuyết cần ghi nhớ và các dạng bài tập thường gặp
có khắc phục đươc vấn đề bạn tìm hiểu ko?, nếu ko hãy comment góp ý thêm về Bất đẳng thức Cô-si: Lý thuyết cần ghi nhớ và các dạng bài tập thường gặp
bên dưới đểHọc viện Anh ngữ toàn diện NYSE có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: nyse.edu.vn của Học viện Anh ngữ toàn diện NYSE

Nhớ để nguồn bài viết này: Bất đẳng thức Cô-si: Lý thuyết cần ghi nhớ và các dạng bài tập thường gặp
của website nyse.edu.vn

Chuyên mục: Giáo dục

[expander_maker more=”Xem thêm chi tiết về Bất đẳng thức Cô-si: Lý thuyết cần ghi nhớ và các dạng bài tập thường gặp
” less=”Read less”]