Công thức tính thể tích khối cầu (hình cầu) Đầy Đủ & Chính Xác nhất

Bạn đang xem:
Công thức tính thể tích khối cầu (hình cầu) Đầy Đủ & Chính Xác nhất
tại nyse.edu.vn

Phương pháp tính thể tích khối cầu đầy đủ và chính xác

Trong bài viết này, trường THPT Chuyên Lê Hồng Phong sẽ giải và chia sẻ cụ thể với bạn đọc một cách đầy đủ và chính xác nhất về cách tính từng phần (phần) và các dạng bài toán thường gặp. Chúng tôi mời bạn khám phá những gì quan trọng nhất!

I. GIAI ĐOẠN NỮ

1. Hình tròn là gì?

Bạn xem: Cách tính khối lượng chi tiết (phần) đầy đủ và chính xác nhất

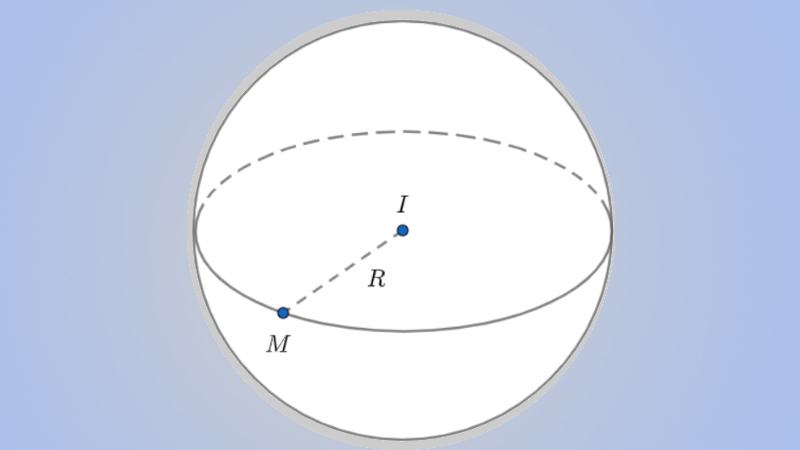
Diện tích: Có một điểm I cố định trong không gian, đường bao của một điểm A cách IA một khoảng cố định gọi là mặt cầu có tâm I, bán kính R = IA.

2. Tòa án là gì?

Mặt cầu: Phần bên trong của một mặt cầu được gọi là mặt cầu hay mặt cầu có tâm I và bán kính R = IA.

II. THỂ TÍCH SAU BỀ MẶT (Hình cầu)

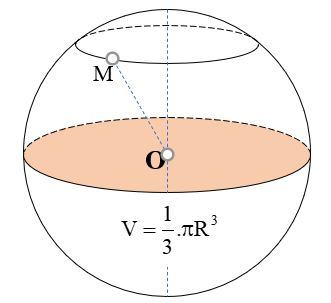
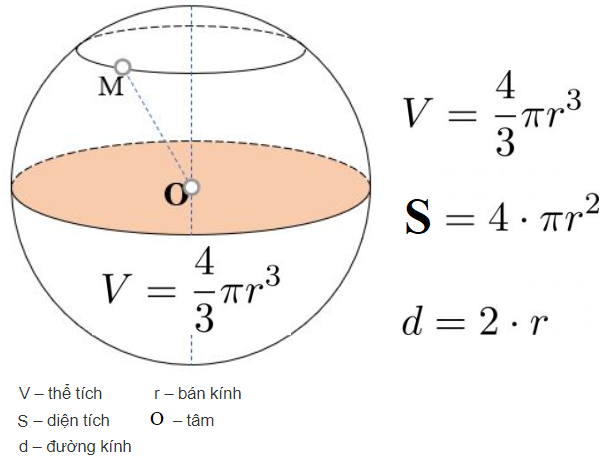
Để tính thể tích của một hình tròn, chúng ta cần tìm kích thước bán kính của nó. Sau đó nhập công thức V = ⁴⁄₃πr³ để tính. Nhớ viết đơn vị thể tích là đơn vị khối (cm3, m3,…)

$V=frac{4}{3} pi .r^{3} =frac{1}{6}pi .d^{3}$

Trong đó:

V là thể tích của đơn vị (đơn vị m3)
là số pi, xấp xỉ 3,14
r là bán kính quay vòng
d là bánh xe quay/quay

**** HỎI NƠI LỢI ÍCH

Công thức tính góc pha là S = 4π.R2.

**** TÓM LƯỢC QUYỀN LỢI DÀNH CHO BẠN

III. CÁCH TÍNH THỂ TÍCH CỦA MỘT HÌNH CẦU (Hình cầu)

Để giải bài toán tính thể tích của một chi tiết (bộ phận), em làm ba bước sau!

Bước 1: Viết công thức tính thể tích hình tròn ra giấy

V = r³

Bước 2: Tìm độ lớn của bán kính

Nếu có một độ dài nhất định trong vấn đề, thì chúng ta chuyển sang bước tiếp theo.

Nếu vấn đề lớn, hãy chia đôi để có được bán kính. Ví dụ đường kính d = 10 cm thì bán kính r = 5 cm.

Bước 3: Nhập công thức tính đơn vị phần trăm

Ví dụ, tìm bán kính r = 5 cm. Chúng ta có,

Diện tích của V = ⁴⁄₃πr³ = 4/3.3,14.(5)³ = 523,3 cm³

IV: HÀM THỂ TÍCH TOÀN CẦU (Hình cầu)

Câu 1: Cho hình tròn có chu vi 31,4 cm. Tìm thể tích của một đoạn có độ dài bằng chu vi của hình tròn đã cho.

Phần thưởng:

Chu vi hình tròn C = 2πr = 31,4 cm

=> Bán kính r = C/2π = 5 cm

Khối lượng của một đơn vị nhất định là:

V = r³ = 4/3.3.14.(5)³ = 523,3 cm³

Câu 2: Tìm thể tích hình tròn đường kính d = 4 cm.

Phần thưởng:

Bán kính r = d/2 = 2 cm

Thể tích của quả cầu là:

V = r³ = 4/3.3.14.(2)³ = 33,49 cm³

Câu 3: Cho tứ diện đều ABCD có cạnh a. Thể tích diện tích tứ diện ABCD là:

$A. frac{pi {{a}^{3}}sqrt{6}}{8}$	$B. frac{pi {{a}^{3}}sqrt{6}}{6}$
$C. frac{pi {{a}^{3}}sqrt{6}}{4}$	$D.frac{3pi {{a}^{3}}sqrt{6}}{8}$

Câu 4: Cho hình chóp tứ giác S.ABCD có đáy là A, góc giữa các cạnh bên và đáy là ${{45}^{0}}$ . Chu vi hình chóp S.ABCD bằng:

$A. frac{9pi {{a}^{2}}}{4}$	$B. frac{4pi {{a}^{2}}}{3}$
$C. frac{3pi {{a}^{2}}}{4}$	$D. frac{2pi {{a}^{2}}}{3}$

Câu 5: Cho hình chóp tứ giác S.ABCD có đáy và các cạnh bằng a. Chu vi của kim tự tháp này bằng:

$A. asqrt{2}$	$B. frac{asqrt{2}}{2}$
$C. asqrt{3}$	$D. frac{asqrt{3}}{3}$

Câu 6: Thể tích phần diện tích nội tiếp hình lập phương cạnh a là:

$A. frac{1}{2}pi {{a}^{2}}$	$B.frac{2}{9}pi {{a}^{2}}$
$C. frac{2}{3}pi {{a}^{2}}$	$D. frac{sqrt{3}}{6}pi {{a}^{2}}$

Câu 7: Cho lăng trụ đứng tam giác đều có đáy và đáy bằng a. Diện tích thiết diện qua trục lăng trụ này bằng:

$A. frac{7}{3}pi {{a}^{2}}$	$B. frac{7}{12}pi {{a}^{2}}$
$C. frac{7}{36}pi {{a}^{2}}$	$D. frac{7}{9}pi {{a}^{2}}$

Câu 8: Thể tích của hình lập phương có cạnh a là:

$A. frac{sqrt{3}pi {{a}^{3}}}{2}$	$B. frac{sqrt{3}pi {{a}^{3}}}{8}$
$C. frac{3sqrt{3}pi {{a}^{3}}}{2}$	$D. frac{pi {{a}^{3}}}{6}$

Câu 9: Cho (S) là mặt cầu có tâm O, bán kính r, d và khoảng cách từ O đến mặt phẳng (P) là d.

A. Không đếm được	b.1
c.0	thua 2

Câu 10: Cho hình vuông có diện tích bằng $frac{8pi {{a}^{2}}}{3}$ . Khi đó bán kính của mặt cầu là:

$A. frac{asqrt{3}}{3}$	$B. frac{asqrt{6}}{3}$
$C.frac{asqrt{6}}{2}$	$D. frac{asqrt{2}}{3}$

Câu 11: Cho hình tròn có thể tích bằng $frac{8pi {{a}^{3}}sqrt{6}}{17}$ . Khi đó độ dài của miền bằng:

$A. frac{asqrt{6}}{2}$	$B. frac{asqrt{6}}{3}$
$C. frac{asqrt{3}}{3}$	$D. frac{asqrt{2}}{3}$

Câu 12: Cho tứ diện DABC, đáy ABC là tam giác vuông tại B, DA vuông góc với mặt đáy. Xác định AB = 3a, BC = 4a, DA = 5a. Bán kính của hình chóp DABC có bán kính bằng:

$A. frac{5asqrt{2}}{2}$	$B. frac{5asqrt{2}}{3}$
$C. frac{5asqrt{3}}{2}$	$D. frac{5asqrt{3}}{3}$

Câu 13: Cho hình chóp tứ giác đều S.ABCD có đáy và các cạnh bên bằng a. Diện tích đường tròn ngoại tiếp hình chóp S.ABCD là

$A. 2pi {{a}^{2}}$	$B. pi {{a}^{2}}$
$C. 4pi {{a}^{2}}$	$D. 6pi {{a}^{2}}$

Trên đây trường THPT Chuyên Lê Hồng Phong đã giới thiệu đến quý thầy cô và các em học sinh công thức tính số đơn vị (phần) và các bài toán thường gặp đầy đủ và chính xác nhất. Chúng tôi hy vọng chúng tôi đã cung cấp cho bạn thông tin hữu ích. Cách tính lượng kim tự tháp cũng được chúng tôi chia sẻ chi tiết. Tìm hiểu thêm!

Tác giả: Học viện Anh ngữ toàn diện NYSE

Thể loại: Giáo dục

Bài chia sẻ: https://c3lehongphonghp.edu.vn https://c3lehongphonghp.edu.vn/cong-thuc-tinh-the-tich-khoi-cau-hinh-cau-day-du-chinh-xac-nhat/

Bạn thấy bài viết
Công thức tính thể tích khối cầu (hình cầu) Đầy Đủ & Chính Xác nhất
có khắc phục đươc vấn đề bạn tìm hiểu ko?, nếu ko hãy comment góp ý thêm về
Công thức tính thể tích khối cầu (hình cầu) Đầy Đủ & Chính Xác nhất
bên dưới đểHọc viện Anh ngữ toàn diện NYSE có thể thay đổi & cải thiện nội dung tốt hơn cho các bạn nhé! Cám ơn bạn đã ghé thăm Website: nyse.edu.vn của Học viện Anh ngữ toàn diện NYSE

Nhớ để nguồn bài viết này:
Công thức tính thể tích khối cầu (hình cầu) Đầy Đủ & Chính Xác nhất
của website nyse.edu.vn

Chuyên mục: Giáo dục

[expander_maker more=”Xem thêm chi tiết về
Công thức tính thể tích khối cầu (hình cầu) Đầy Đủ & Chính Xác nhất
” less=”Read less”]